2진수
2진수는 2를 기반으로 하는 숫자체계로서, 컴퓨터 내에서 데이터를 표현하기 위해 사용된다. 2 진수는 "0"과 "1"이라는 오직 2가지 종류의 숫자로만 구성된다.
비트란 이진법의 최소단위로, 숫자 0,1로 신호를 나타내는 최소의 단위를 비트라 합니다. 비트를 가지고 수학적 연산을 하기 위해, 컴퓨터는 2진수라는 수 체계를 사용한다.
수체계
우리가 사용하는 수 체계는 10진수이다. 10진수는 0부터 9까지 10개의 숫자를 이용하여 값을 표현할 수 있다. 10진수에서 각 자리는 10의 거듭제곱을 나타낸다.
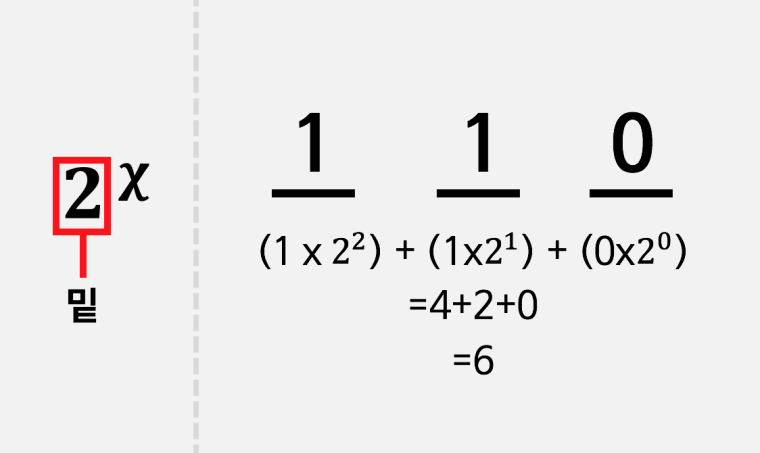
가장 오른쪽 수는 1의 자릿수(10^0100 ). 오른쪽에서 두 번째 수는 10의 자릿수(10^1101 ). 오른쪽에서 세 번째 수는 100의 자릿수(10^2102 )
컴퓨터는 전기적 신호 켜짐(1)과 꺼짐(0)을 이용하여 작동하기 때문에 2진수를 사용한다. 2진수는 0부터 1까지 2개의 숫자를 이용하여 값을 표현할 수 있다.
가장 오른쪽 자리의 수는 아직 1의 자릿수(2^020 ). 그 옆의 자리의 수는 2의 자릿수(2^121 ). 그 다음 자리의 수는 4의 자릿수(2^222 )인 방식으로 계속 나아간다. 2진수의 값을 계산하려면, 각 자리의 수와(0또는 1) 각 자릿수를 곱하여 전부 더하면 된다. 그러므로 110은 (1×4)+(1×2)+(0×1)=4+2+0=6이다

.
2진수에서 숫자 세는 방법
2진수로 숫자를 세는 방법은 10진수에서 숫자를 세는 방법과 비슷하지만 0과 1 두 개의 수로만 제한된다는 차이가 있다. 따라서 0을 2진수로 바꾸면 여전히 0이고, 1을 2진수로 바꾸면 여전히 1이다.
그러나 2진수에서는 10진수 2를 사용할 수 없으므로 2를 나타내기 위해서는 또 다른 비트가 필요하고, 10진수 2는 2진수 10으로 나타낸다. 1이 2의 자릿수에 있고 0이 1의 자릿수에 있으므로, 10진수 2의 2진수 값은 2×1+1×0=2고, 10진수 3의 2진수는 11이다.
하지만 숫자 4를 나타내기에는 또 비트가 모자르게된다. 10진수 4를 나타내기 위해 3번째 비트가 추가로 필요하다. 10진수 4는 2진수 값으로 나타내면, 100(4×1+ 2×0+1×0)이다.
10진수 체계에 적용하는 수학을 2진수에도 적용할 수 있다. 10진수에서와 마찬가지로 2진수에서도 셈, 더하기, 빼기, 곱하기, 나누기를 할 수 있고 컴퓨터는 연산과 계산을 할 때 이런 수학을 사용한다.
'CS > 컴퓨터' 카테고리의 다른 글
| [컴퓨터 기초] 16진수(hexadecimal) (0) | 2021.08.20 |
|---|---|
| [컴퓨터 기초] 32bit 컴퓨터와 64bit 컴퓨터 차이점 (0) | 2021.08.17 |
| [컴퓨터 기초] bit, byte (0) | 2021.08.17 |
| [컴퓨터 기초] 하드웨어 (0) | 2021.08.17 |
| [컴퓨터 기초] ASCII Code(아스키코드) (0) | 2021.03.20 |